The video demonstrates how the complex motion of a double pendulum can be simulated using differential equations solved via Euler’s method with Taylor series expansions, highlighting how truncating these series and computational limitations lead to accumulating errors. It also provides an intuitive explanation of Taylor series and their physical significance in the system, showing that higher-order terms improve simulation accuracy at the cost of increased computational effort.
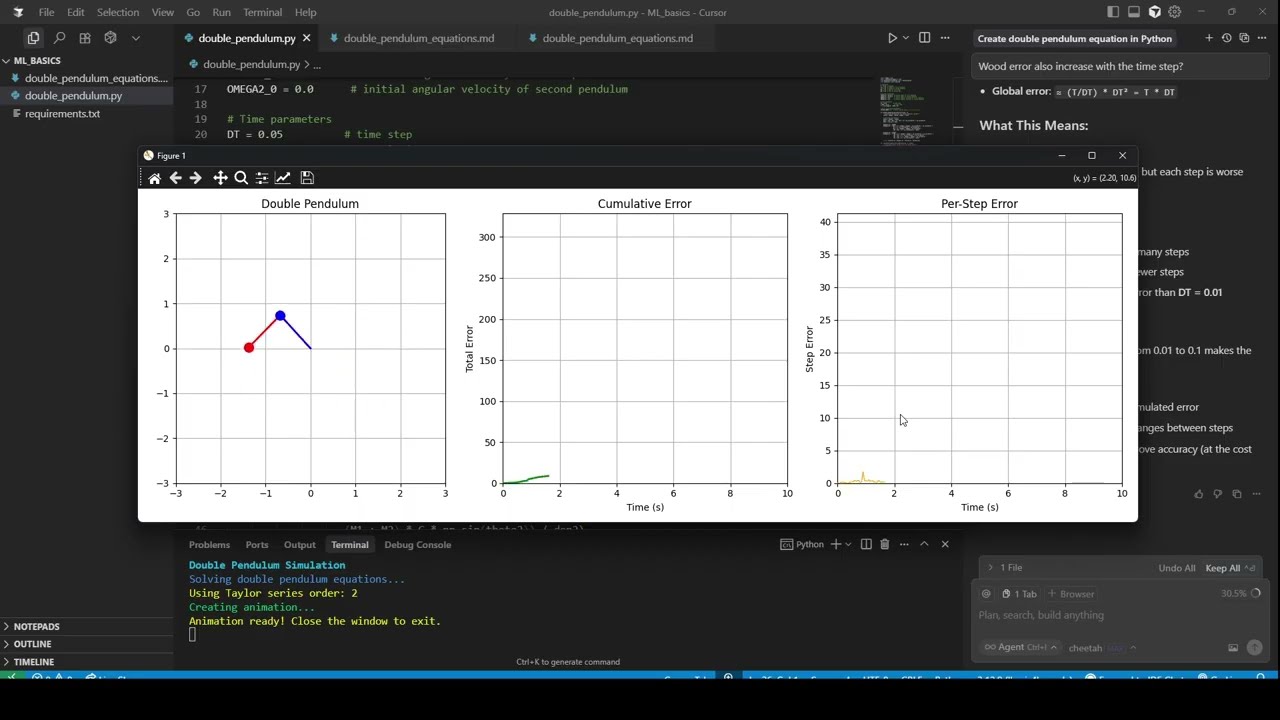
In this video, the presenter explores the fascinating dynamics of a double pendulum system and how its motion can be accurately simulated using differential equations and Taylor series expansions. The double pendulum’s swinging motion is shown alongside charts that track cumulative and stepwise errors occurring during the numerical simulation. The core mathematical model involves second-order ordinary differential equations, which are approximated using Taylor series expansions truncated at various orders. The presenter explains that while an infinite Taylor series would perfectly model the system, practical computations require truncation, which inevitably leads to accumulating errors.
The video delves into the role of Taylor series in approximating the pendulum’s motion. Taylor series are infinite sums of polynomial terms derived from a function’s derivatives at a specific point, allowing smooth functions to be approximated locally. In this simulation, truncating the series at the third derivative (second order) introduces errors that accumulate over time. The presenter highlights that these errors are unavoidable not only because of the truncation but also due to the limitations of computer decimal precision. Additionally, the choice of time step in the numerical method affects both the simulation speed and the error magnitude, with smaller time steps generally reducing error accumulation.
Euler’s method is used as the numerical technique to solve the differential equations, and it is based on truncated Taylor series expansions. By increasing the order of the Taylor series used in Euler’s method, the simulation’s accuracy improves, and error accumulation slows down. The presenter demonstrates this by running the simulation with higher Taylor series orders, showing a noticeable reduction in error spikes and overall error growth. This illustrates how considering more terms in the Taylor series leads to better approximations of the pendulum’s motion, although computational complexity also increases.
Beyond the simulation, the presenter provides an intuitive explanation of Taylor series and their significance. Taylor series approximate any smooth function using polynomials by leveraging derivatives at a point. The video touches on related concepts like the Maclaurin series (a special case centered at zero) and explains how derivatives correspond to physical quantities in the pendulum system: the first derivative relates to velocity, the second to acceleration, and the third to jerk (the rate of change of acceleration). This layered understanding helps visualize how the pendulum’s position evolves over time and why higher-order derivatives improve the accuracy of the simulation.
Finally, the presenter reflects on the broader implications and excitement of applying mathematical concepts like Taylor series and differential equations to real-world physical systems. They mention the use of Python’s Matplotlib library for animating the pendulum and experimenting with parameters such as pendulum lengths and Taylor series order. The video encourages viewers to appreciate the interplay between mathematics, physics, and computational methods, even if the detailed equations seem daunting. The presenter plans to share the code and further insights on a Patreon post, inviting others to explore and learn alongside them.