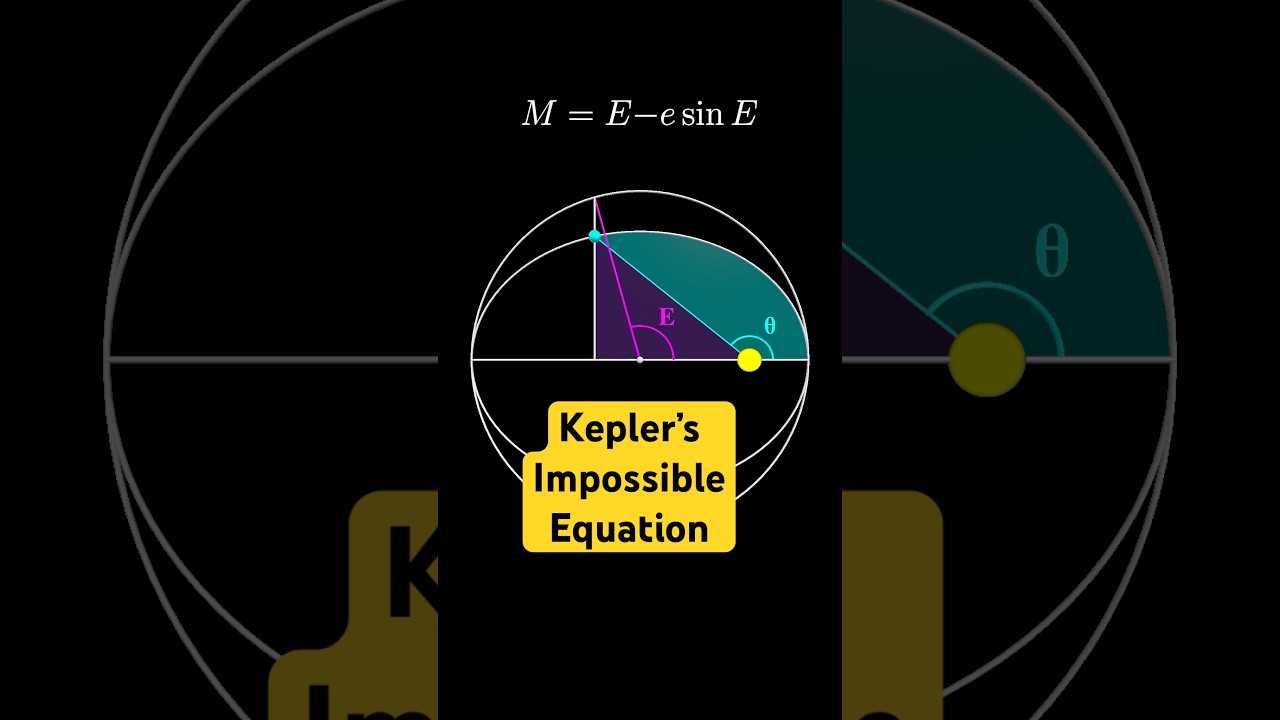
The video explores Kepler’s Impossible Equation, which relates to the motion of planets in elliptical orbits and highlights the challenges in deriving useful equations for predicting planetary positions. Despite Kepler’s significant contributions in the 17th century, the quest to solve his equations continues, with recent attempts in 2024 reflecting the ongoing interest in understanding planetary motion.
The video discusses Kepler’s Impossible Equation, which relates to the motion of planets in elliptical orbits. Kepler’s laws of planetary motion state that planets sweep out equal areas in equal times, but to utilize this principle for practical astronomy, one must compute the angle Theta that a planet makes with the body it is orbiting. The video illustrates how to inscribe Kepler’s ellipse within a circle to demonstrate the relationship between the area swept out by the planet and the area that would be swept out in a circular orbit.
To derive useful equations from this relationship, the video presents a series of algebraic manipulations that lead to two key equations. The first equation connects time to the central angle, denoted as e, while the second equation relates e to the angle Theta. These equations are crucial for predicting the position of a planet at a future time, which is essential for astronomical calculations.
Despite Kepler’s groundbreaking discoveries in the early 17th century, he was unable to solve the equations he formulated. This inability to find a solution has posed a challenge for astronomers and mathematicians for centuries. The video emphasizes that the quest to solve Kepler’s equation has continued into modern times, with ongoing attempts to find a resolution.
The video highlights a recent attempt from 2024 to tackle this longstanding problem, showcasing the enduring interest in Kepler’s work and its implications for understanding planetary motion. The challenge of solving Kepler’s equation remains a significant topic in both historical and contemporary astronomy.
In conclusion, the video invites viewers to engage with the topic further by liking and subscribing for more content. It underscores the importance of Kepler’s discoveries and the ongoing efforts to solve the equations that describe planetary motion, reflecting the intersection of history, mathematics, and astronomy.