The video discusses the fundamental limitations of current deep learning models, particularly their inability to perform true algorithmic reasoning, and argues that geometric deep learning, while helpful, is inherently restricted by its reliance on symmetries. It proposes that category theory could provide a more general and principled mathematical framework for designing neural networks, enabling them to handle complex computations and generalize more effectively.
Certainly! Here’s a five-paragraph summary of the video, with spelling and grammar corrected for clarity:
The video begins by highlighting a fundamental limitation of current deep learning models, particularly large language models (LLMs): they struggle with basic algorithmic tasks like addition and multiplication. While LLMs can often mimic correct answers by recognizing patterns, they fail when presented with slightly altered or unfamiliar problems, revealing that they do not truly internalize algorithmic reasoning. This limitation extends to other domains, such as physics, where models can approximate but not fully encapsulate fundamental laws. The discussion emphasizes that simply connecting LLMs to external tools (like calculators) is not a complete solution, as it introduces inefficiencies and fails to address the underlying architectural shortcomings.
The conversation then shifts to geometric deep learning, which builds neural networks to be equivariant to symmetry transformations—meaning the model’s output remains consistent under certain input transformations, like shifting an image. This approach has been powerful in reducing data requirements and improving generalization, especially for structured data like graphs. However, geometric deep learning is fundamentally limited because it relies on invertible transformations (symmetries), which do not capture the full range of computations, especially those that destroy or compress information, such as many classical algorithms.
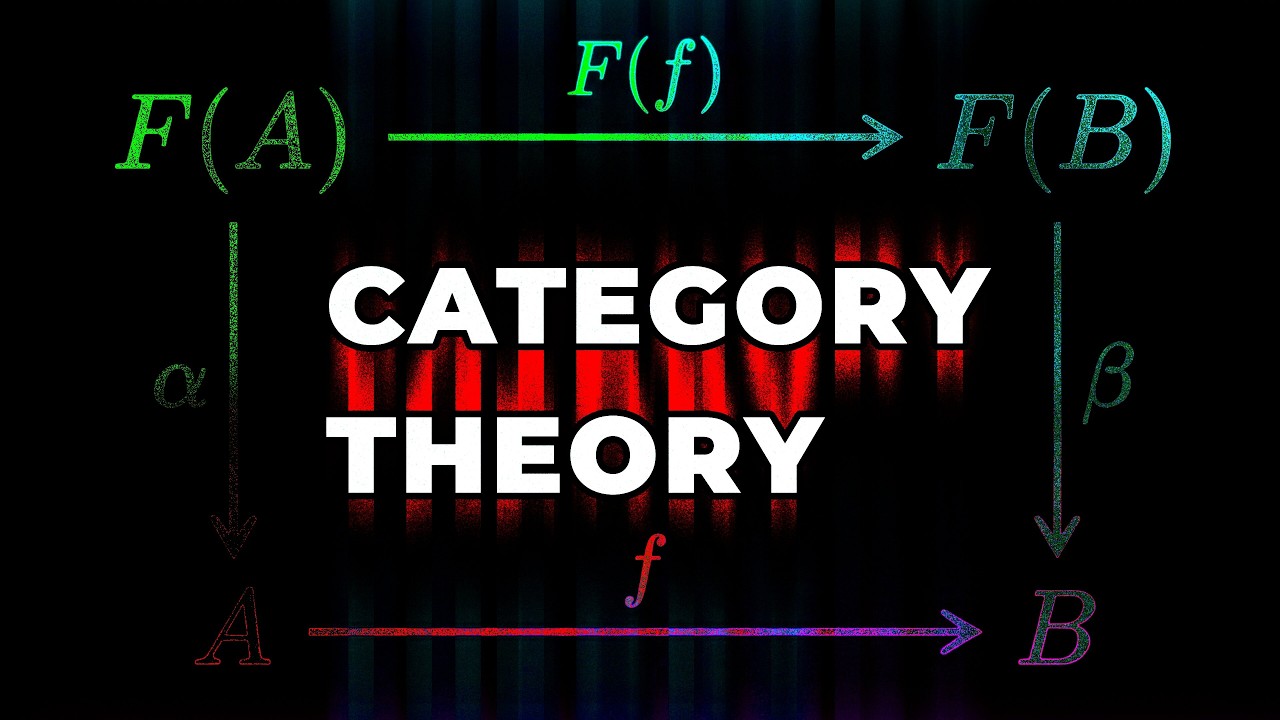
To address these limitations, the video introduces category theory as a more general mathematical framework. Category theory allows for the description of structures and relationships (morphisms) between objects in a way that can encompass both invertible and non-invertible computations. This abstraction enables the modeling of more complex computational structures, such as lists, trees, and recursive data types, which are common in computer science but not easily handled by group-based geometric deep learning. The concept of higher categories (like two-categories) is introduced to formalize relationships not just between objects, but also between the relationships themselves, which is crucial for understanding phenomena like weight sharing in neural networks.
The speakers argue that categorical deep learning could provide the unifying theoretical foundation that deep learning currently lacks. Unlike the current ad hoc design of neural architectures, category theory offers a systematic way to reason about compositionality, recursion, and structure-preserving transformations. This could lead to more principled neural network designs that are capable of robust algorithmic reasoning, better integration with symbolic computation, and improved generalization beyond the training distribution. The analogy is made to the periodic table in chemistry: just as the periodic table provided a principled foundation for chemistry, categorical deep learning could do the same for neural networks.
In conclusion, the video suggests that the future of deep learning lies in bridging the gap between constraints (theoretical requirements) and implementation (practical neural architectures) using category theory. This approach not only generalizes geometric deep learning but also naturally incorporates essential computational concepts like recursion, weight tying, and non-invertible operations. The presenters encourage viewers to explore their formal work on categorical deep learning, which aims to provide a universal algebraic framework for neural networks, potentially leading to more powerful and reliable AI systems.