The video explores the common misconception that training large AI models like Meta’s Llama 3.2 involves simply descending a loss landscape to find the lowest point, akin to walking downhill in a mountain. It highlights how early AI pioneers, including Jeff Hinton, doubted the effectiveness of gradient descent due to fears of getting stuck in local minima. However, modern understanding shows that gradient descent works remarkably well, especially in high-dimensional spaces, although visualizing this process remains challenging. The series aims to provide a visual and intuitive understanding of how large models learn, emphasizing that their training process resembles falling through a wormhole rather than straightforward downhill movement.
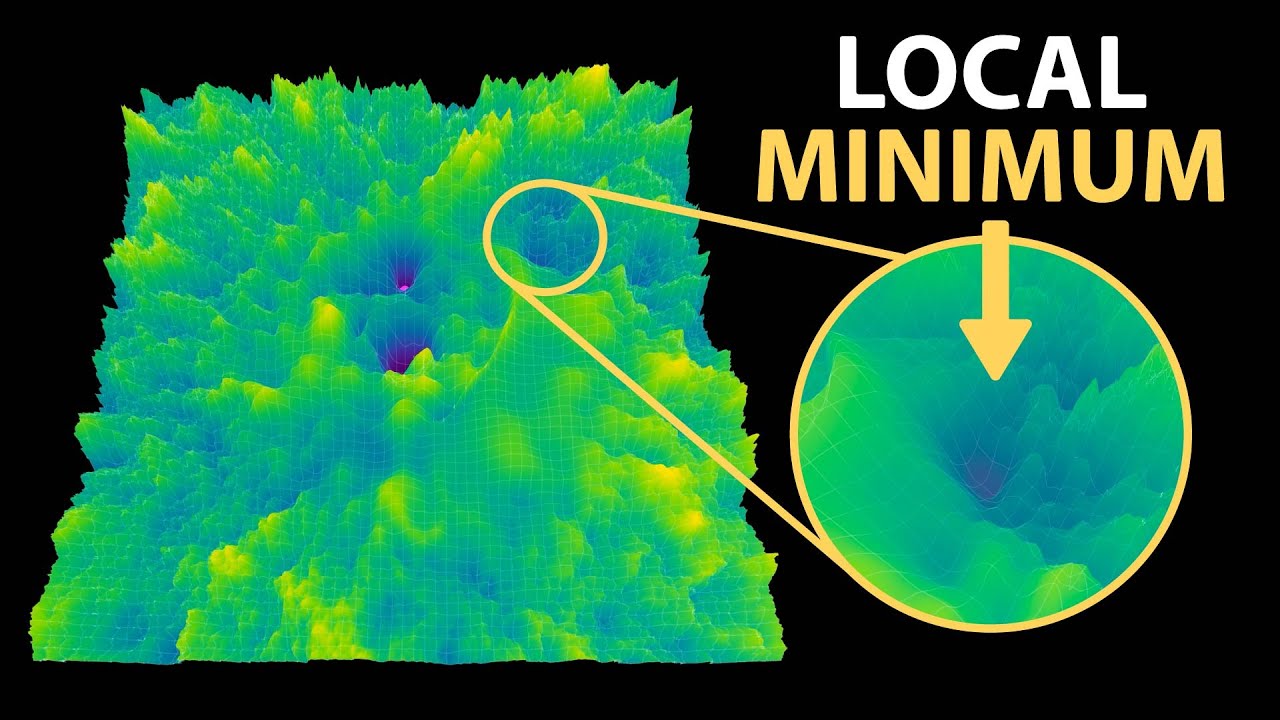
The video explains how language models like Llama are trained to predict the next token in a sequence, using probabilities and loss functions such as cross entropy to measure performance. It demonstrates how individual model parameters influence predictions and how adjusting these parameters can improve confidence in correct tokens. Visualizations of the loss landscape for a few parameters reveal that the loss surface is highly complex, with many hills and valleys. Importantly, the landscape’s shape changes as the model learns, illustrating that the training process involves navigating a high-dimensional, dynamic terrain rather than a static, simple surface.
A key insight presented is that the high-dimensional loss landscape of models with billions of parameters cannot be fully visualized or optimized by tuning one or a few parameters at a time. Instead, gradient descent uses the gradient—a vector indicating the steepest descent direction—to iteratively move toward lower loss regions. The process is akin to following a downhill slope in a forest without a map, where the gradient guides the model toward better solutions. Visualizations of random directions in the high-dimensional space show that the landscape contains many hidden valleys and peaks, which become more accessible as the model trains and the landscape shifts.
The most surprising revelation is that, contrary to the initial intuition, gradient descent in high-dimensional spaces does not get stuck in local minima as often feared. Instead, the process resembles a wormhole opening in the loss landscape, rapidly transporting the model’s parameters into a deep valley that was previously hidden. This phenomenon occurs because moving in the full high-dimensional space alters the shape of the loss landscape itself, revealing better solutions that are invisible when only considering a few parameters. The video emphasizes that the true learning process involves navigating this complex, high-dimensional terrain, which is far more intricate than simple visualizations suggest.
Finally, the video discusses how visualizing the loss landscape in just a few dimensions provides limited insight into the actual training process of large models. As models grow in size, their loss landscapes become increasingly complex and difficult to interpret visually. Nonetheless, the mathematics behind gradient descent remains robust, allowing models to efficiently find optimal solutions despite the high dimensionality. The creator also shares a poster featuring visualizations of various models’ loss landscapes, highlighting differences between pre-trained and instruction-tuned models, and offers it for sale. Overall, the series aims to demystify the learning process of large AI models, showing that their success hinges on navigating a high-dimensional, dynamic landscape that is far more complex than traditional visualizations can capture.
