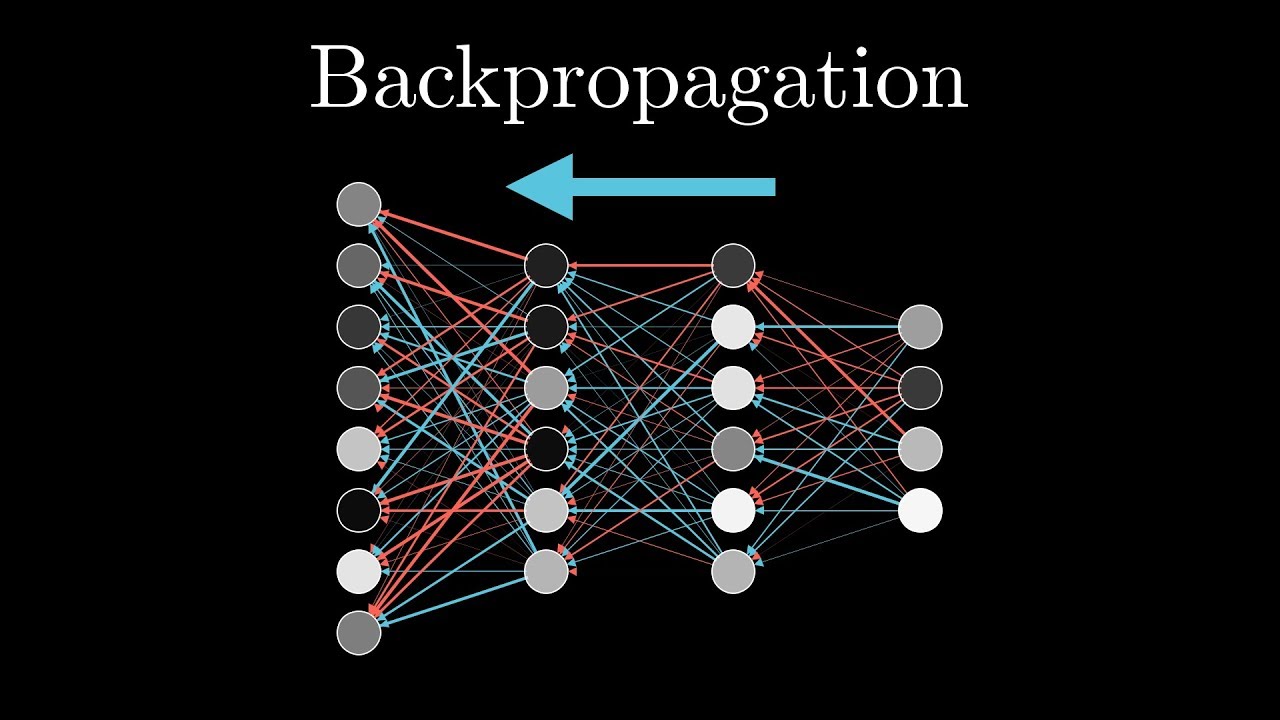
The video explores backpropagation as the fundamental algorithm for neural network learning, focusing on adjusting weights and biases to minimize the cost function efficiently. It discusses the intuition behind backpropagation, emphasizing the importance of understanding how individual training examples influence weight and bias adjustments to guide the network towards accurate predictions.
In the video, backpropagation is discussed as the core algorithm behind how neural networks learn. The video starts by providing a quick recap of neural networks and gradient descent, setting the stage for understanding backpropagation. The example given involves recognizing handwritten digits, with a network consisting of input and output layers, as well as two hidden layers. The goal of backpropagation is to compute the gradient of the cost function, indicating how weights and biases should be adjusted to minimize the cost efficiently.
The video explains the intuition behind backpropagation without delving into complex mathematical formulas. It emphasizes the idea that the gradient provides information on how sensitive the cost function is to changes in weights and biases. By understanding the relative sensitivity of each component, adjustments can be made proportionally to achieve a rapid decrease in cost. The process involves considering the impact of individual training examples on weight and bias adjustments, with a focus on nudging the network towards correct classifications.
The concept of neurons firing together wire together, inspired by Hebbian theory in neuroscience, is introduced to explain how connections are strengthened between active neurons. The video breaks down how adjustments to weights, biases, and activations in each layer contribute to changing the network’s behavior. The backpropagation process involves propagating desired changes from the output layer back through the network, considering the collective impact of all training examples to update weights and biases.
To improve computational efficiency, mini-batch stochastic gradient descent is introduced as a practical way to approximate the gradient descent step. By randomly shuffling and dividing training data into mini-batches, adjustments are made based on subsets of examples rather than the entire dataset. This approach speeds up the learning process while still converging towards a local minimum of the cost function. Overall, backpropagation is explained as the algorithm for determining how individual training examples influence weight and bias adjustments to guide the network towards accurate predictions.
The video concludes by highlighting the importance of having sufficient training data for backpropagation to work effectively. Using the MNIST database as an example, the challenge of obtaining labeled training data is emphasized as a common hurdle in machine learning tasks. Understanding the mechanics of backpropagation, including how adjustments are made based on individual training examples and the role of gradient descent in updating weights and biases, provides a foundational understanding of how neural networks learn and improve their performance.